One of the big punchlines of classical probability is that the probability of the sample space \(S\) is 1 (100%), i.e. 

\[P(S)=\frac{n(S)}{n(S)}=\frac{|S|}{|S|}=1\]

in words: "The probability something happens is 100%"

Now for an event \(E\) 

We then have the following relationship with the probability of \(\overline{E}\) and the probability of \(E\) 

\[P(\overline{E})=1-P(E)\]

Mathematically this can be seen as

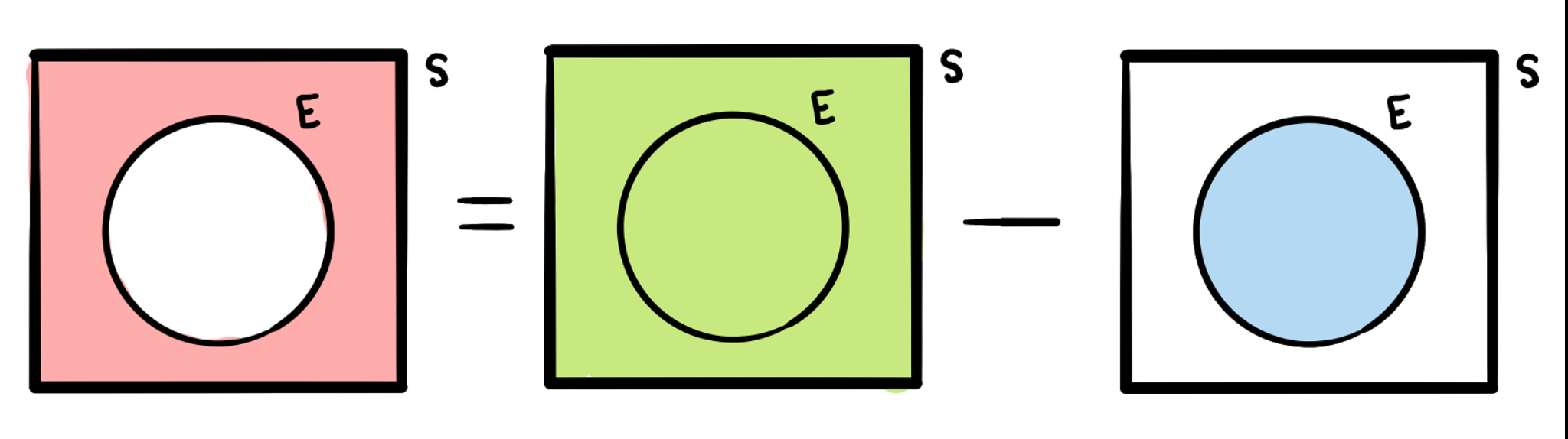
\[|E|+\left|\overline{E}\right|=|S|\]